AoC 2025
My solutions for Advent of Code 2025
Welcome to my solution page for Advent of Code 2025. They are all in Clojure, you can find the git repo here. I’m rather new to Clojure—if you see any improvements, please don’t hesitate to contact me via email (something@myname.nl) or create an issue.
Day 1: Secret Entrance
Part 1
We convert the input into numbers (L68 would be -68, R34 would be 34).
(defn convert-rotation "Converts a rotation string into a number.
For example, L68 would be -68, and R48 would be 48."
[rot]
(let [direction (first rot)
number (Integer/parseInt (subs rot 1))]
(condp = direction
\L (- number)
\R number)))For part one we simply compute the entire list of numbers via (reductions + 50 rotations) and check how many are zero modulo 100.
(defn part1 [input]
(->> input
s/parse-lines
(map convert-rotation)
(reductions + 50)
(map #(mod % 100))
(filter zero?)
count))Part 2
We now also have to count how often the dial moves across 0. We do this via the function zero-counters, which takes two numbers: before and after moving the dial (from and to). A couple of example movements with the corresponding amount of zeros seen:
- \(105 \rightarrow 301 = 2\)
- \(-101 \rightarrow 100 = 3\)
- \(-155 \rightarrow -100 = 0\)
- \(-9900 \rightarrow -9925 = 0\)
Thinking a bit about this, we can divide both from and to by 100 and take the difference. Whether we take the floor or ceiling division depends on whether from or to is higher. With zero-counters done it’s straightforward:
(defn- zero-counters
"When moving the dial from `from` to `to`, how often does the dial
point at `0`, during or after the rotation?"
[from to]
(let [divver (if (< from to) #(Math/floorDiv %1 %2) #(Math/ceilDiv %1 %2))]
(let [a (divver from 100)
b (divver to 100)]
(Math/abs (- b a)))))
(defn part2 [input]
(->> input
s/parse-lines
(map convert-rotation)
(reductions + 50)
(partition 2 1)
(pmap (fn [[x y]] (zero-counters x y)))
(reduce +)))Day 2: Gift Shop
Part 1
Regex with backtrace, match a number twice for part one
(defn- to-ranges
"Converts todays puzzle input to a seq of float-pairs.
For example, \"11-22,95-115\" will be converted to ((11 22) (95
115))."
[input]
(->> input
u/to-csvs
u/parse-ranges))
(defn solve
[input regexp]
(->> input
to-ranges
(pmap (fn [[start end]]
(filterv #(re-matches regexp (str %))
(range start (inc end)))))
flatten
(reduce +)))(defn part1 [input] (solve input #"^(\d+)\1$"))Part 2
And simply match it more often for Part 2
(defn part2 [input] (solve input #"^(\d+)\1+$"))Day 3: Lobby
Part 1
I stole Mikkels idea, which is simple but I totally missed it in my first attempt.
If \(n\) is the desired amount of batteries (\(n=2\) for Part 1), and \(i\) is the amount of batteries you have already included, you should not look at the last \(k = n-i\) numbers, because otherwise you run out of space. (drop-last (dec k))
Now, in order to determine the first battery, you just use the maximum value \(m\) in the list of batteries (remember, with the last \(k\) batteries removed)! Easy peasy!
In order to determine the second battery, you remove the battery you just used, and look at the new \(m\) again. Easy peasy! Removing this battery is done by removing all leading batteries \(b\) where the value of \(b\) is lower than \(m\), and removing one more ((rest (drop-while #(< % max)))).
(defn- result [line n]
(last
(reduce
(fn [[current val] k]
(let [max (->> current
(drop-last (dec k))
(apply max))
new-bank (->> current
(drop-while #(< % max))
rest)]
[new-bank (+ max (* 10 val))]))
[line 0]
(range n 0 -1))))
(defn- solve [input n]
(->> input
u/to-lines
(map u/->digits)
(pmap #(result % n))
(reduce +)))(defn part1 [input] (solve input 2))Part 2
\(n=12\):
(defn part2 [input] (solve input 12))Day 4: Printing Department
We use a couple of util functions here. Click on utils.clj to see them - they are inspired by Darren Austin.
Part 1
Rather straightforward, (grid/locs-where grid #(= \@ %) returns all rolls. Loop over them and see how many neighbours are rolls. Filter for 4 and count.
(defn- removable-rolls [grid]
(->> (g/locs-where grid #(= \@ %)) ; all roll locations
(map (fn [point]
(let [neighs (v/adjacent-to point)
cnt (count (filter #(= \@ (get grid %)) neighs))]
{:point point :neighbours neighs :count cnt})))
;; a roll is `removable` if it has less than 4 rolls as neighb
(filter #(< (:count %) 4))))
(defn part1 [input]
(->> input
g/parse-grid
removable-rolls
count))Part 2
We loop until we’re done, until (empty? to-remove). (assoc g (:point p) \.) effectively removes a roll in the grid (at point p) by setting it to ..
(defn part2 [input]
(let [grid (g/parse-grid input)]
(loop [grid* grid
removed 0]
(let [to-remove (removable-rolls grid*)]
(if (empty? to-remove)
removed
(recur
(reduce (fn [g p] (assoc g (:point p) \.))
grid*
to-remove)
(+ removed (count to-remove))))))))Day 5: Cafetaria
We filter fresh ingredients. For each ingredient, we loop over all ranges and consider the ingredient fresh if any range covers it.
Part 1
(defn- parse-ranges [block]
(->> block
(re-seq #"\d+")
(map parse-long)
(partition 2)))
(defn- fresh? [ingredient ranges]
(some (fn [[start end]]
(and (>= ingredient start)
(<= ingredient end)))
ranges))
(defn part1 [input]
(let [[ranges ingredients] (s/parse-blocks input)
ranges (parse-ranges ranges)
ingredients (s/parse-ints ingredients)]
(->> ingredients
(filter #(fresh? % ranges))
count)))Part 2
The ranges are too big to enumerate so we have to sum the ranges individually. This is very difficult to do if you don’t sort it beforehand, and very easy to do if you do. Thanks for the inspiration, Ruben.
Once sorted, we start with the smallest range and reduce them by storing [current m]. current refers to the current count (which is the puzzle answer after reducing). m refers to the maximum range end at the moment. If a next range starts before m, we don’t count those elements, preventing double-counting overlapping ranges.
(defn part2 [input]
(let [ranges
(->> input
s/parse-blocks
first
parse-ranges
(sort #(< (first %1) (first %2))))]
(first
(reduce (fn [[current m] [from to]]
(if (> from m)
[(+ current (- (inc to) from)) (max m to)]
[(+ current (max 0 (- to m))) (max m to)]))
[0 -1]
ranges))))Day 6: Trash Compactor
Part 1
Part one contains of two parts: parsing and reducing. The parsing is straightforward (effectively just v/transpose)
(defn part1 [input]
(let [inp (s/parse-lines input)
nums (drop-last 1 inp)
cols
(->> nums
(map s/parse-ints)
v/transpose)
ops (str/split (last inp) #" +")]
(result cols ops)))The code above omits result, a function that takes the columns and corresponding operators and computes the final result. We do (zipmap cols ops) to group them nicely together, and then simply reduce.
(defn- result
[cols ops]
(reduce
(fn [acc [col op]]
(+ acc
(condp = op
"*" (reduce * col)
"+" (reduce + col)
))
)
0
(zipmap cols ops)))Part 2
Part two is somewhat similar, except that the parsing is now more difficult. I define group-while, a function that’s quite badly named, suggesting generality while it really is mostly useful for Advent of Code 2025, Day 6, Part 2. Here it is:
(defn group-while
"Groups a collection into subgroups as long as `pred` holds."
[pred coll]
(loop [res [[]]
i 0]
(if (= i (count coll))
res
(let [x (nth coll i)]
(if (pred x)
(recur (assoc res (dec (count res)) (conj (last res) x)) (inc i))
(recur (conj res []) (inc i)))))))And it allows you to group a collection into subcollections. Each element x is kept in a group as long as (pred x) holds. An example shows the result:
(group-while odd? [1 3 5 2 3 5 6 7 8 9])[[1 3 5] [3 5] [7] [9]]For part two, a logical pred is whether the line contains non-whitespace characters. As long as it does, we’re still in the same “problem”. After this we can reduce, where (map #(first (s/parse-ints (str/join %))) row) does the heavy lifting. s/parse-ints parses all integers and throws away the rest (like whitespace or operators). Since it’s already transposed, this is enough - the rest is similar to part one.
(defn part2 [input]
(let [inp (->> (s/parse-lines input)
v/transpose
(group-while (fn [x] (not (every? #(= \space %) x)))))]
(reduce (fn [total row]
(let [op (last (first row))]
(+ total
(condp = op
\* (reduce * (map #(first (s/parse-ints (str/join %))) row))
\+ (reduce + (map #(first (s/parse-ints (str/join %))) row))))))
0
inp)))Day 7: Laboratories
For this we have to appreciate the fantastic meme by ben-guin.
Part 1
For part one we need to find out “how often is the tachyon beam split?”, which is the same question as “how many splitters have a beam directly above them?”. For this we define the function is-beam?, which is defined recursively:
(defn is-beam?
"Returns true when a point in a grid is a beam, nil otherwise.
A point is a beam if and only if at least one of the following
holds:
- 'n' (spot north) is a beam AND NOT a splitter (`^`)
- 'ne' is a beam AND 'e' is a splitter
- 'nw' is a beam AND 'w' is a splitter
- the point points to `S`"
[grid [x y]]
(if (= 0 y)
(= \S (get grid [x y]))
(or (and (is-beam? grid [x (dec y)])
(not (= \^ (get grid [x (dec y)]))))
(and (is-beam? grid [(inc x) (dec y)])
(= \^ (get grid [(inc x) y])))
(and (is-beam? grid [(dec x) (dec y)])
(= \^ (get grid [(dec x) y]))))))This is a classic DP problem, made efficient with memoization:
(def is-beam? (memoize is-beam?))And this makes part one trivial (recall, g/locs-where allows us to easily find out all splitter locations in the grid):
(defn part1 [input]
(let [grid (g/parse-grid input)
splitters (g/locs-where grid #(= \^ %))]
(->> splitters
(filter (fn [[x y]] (is-beam? grid [x (dec y)])))
count)))Part 2
For part two we traverse the grid by going downwards and starting at S, and recursing whenever we encounter a splitter. memoize helps us again.
(defn timelines
"Returns the amount of timelines possible in a grid, start [x y]."
[grid [x y]]
(if (nil? (get grid [x y]))
1
(if (= \^ (get grid [x (inc y)]))
(+ (timelines grid [(dec x) (inc y)])
(timelines grid [(inc x) (inc y)]))
(timelines grid [x (inc y)]))))
(def timelines (memoize timelines))
(defn part2 [input]
(let [grid (g/parse-grid input)
start (first (g/locs-where grid #(= \S %)))]
(timelines grid start)))Day 8: Playground
Part 1
Find all pairs of boxes, compute the distance between each pair of points, sort by distance, take 1000, and do some set/union magic to group into circuits. Sort by count again, take 3 and multiply.
(defn- pairs [xs]
(for [i (range (count xs))
j (range i)]
[(nth xs i) (nth xs j)]))
(defn- distance [[x y z] [x' y' z']]
(Math/sqrt (+ (Math/pow (- x' x) 2) (Math/pow (- y' y) 2) (Math/pow (- z' z) 2))))
(defn part1 [input]
(->> input
s/parse-lines
(mapv s/parse-ints)
pairs
(map (fn [[a b]] [(distance a b) a b]))
sort
(take 1000)
(reduce (fn [sets [distance one two]]
(let [s1 (some #(if (contains? % one) % nil) sets)
s2 (some #(if (contains? % two) % nil) sets)]
(-> (remove
#(or (= s1 %)
(= s2 %)) sets)
(conj (set/union (or s1 #{one}) (or s2 #{two}))))))
[])
(map count)
(sort >)
(take 3)
(reduce *)))Part 2
Loop over all pairs of boxes, combining them at each step. Whenever we end up with only one set, we’re done. Else, continue.
(defn part2 [input]
(let [boxes (->> input
s/parse-lines
(mapv s/parse-ints))
shortest-pairs (->> boxes
pairs
(map (fn [[a b]] [(distance a b) a b]))
sort)]
(loop [sets []
remaining shortest-pairs]
(let [[distance one two] (first remaining)
s1 (some #(if (contains? % one) % nil) sets)
s2 (some #(if (contains? % two) % nil) sets)
new-sets
(-> (remove #(or (= s1 %)
(= s2 %)) sets)
(conj (set/union (or s1 #{one}) (or s2 #{two}))))]
(if (and (= 1 (count new-sets))
(every? (fn [x] (contains? (first new-sets) x)) boxes))
(* (first one) (first two))
(recur new-sets (rest remaining)))))))Day 9: Movie Theater
Part 1
Part one is not too difficult: take all pairs of corners (our input), compute the size of the square, and then just take the largest of those.
(defn- pairs [xs]
(for [i (range (count xs))
j (range i)]
[(nth xs i) (nth xs j)]))
(defn- size [[x y] [x' y']]
(* (inc (abs (- x x')))
(inc (abs (- y y')))))
(defn- largest-square [points]
(reduce
(fn [m [a b]]
(max m (size a b)))
0
(pairs points)))
(defn part1 [input]
(->> input
s/parse-lines
(mapv s/parse-ints)
largest-square))Part 2
I found part two very difficult. After way too long I, again inspired by Mikkel, decided to put my input in desmos, after which I found out that the input is very peculiar, and a solution came to mind, but even then in quite a few iterations.
Our input is a ragged circle, but for a “hole” in the middle. Like a Pacman with an enormously long but narrow mouth. Looking carefully, any rectangle not using the corner points (we call these the outliers) of his mouth will realistically never have a chance of being the biggest, so we can simplify our solution by looking at all rectangeles that use these points.
There’s another insight necessary, however. Let me take out a pen and paper. I’ve drawn the puzzle input in a polygon in blue, and created some imaginary lines in black.
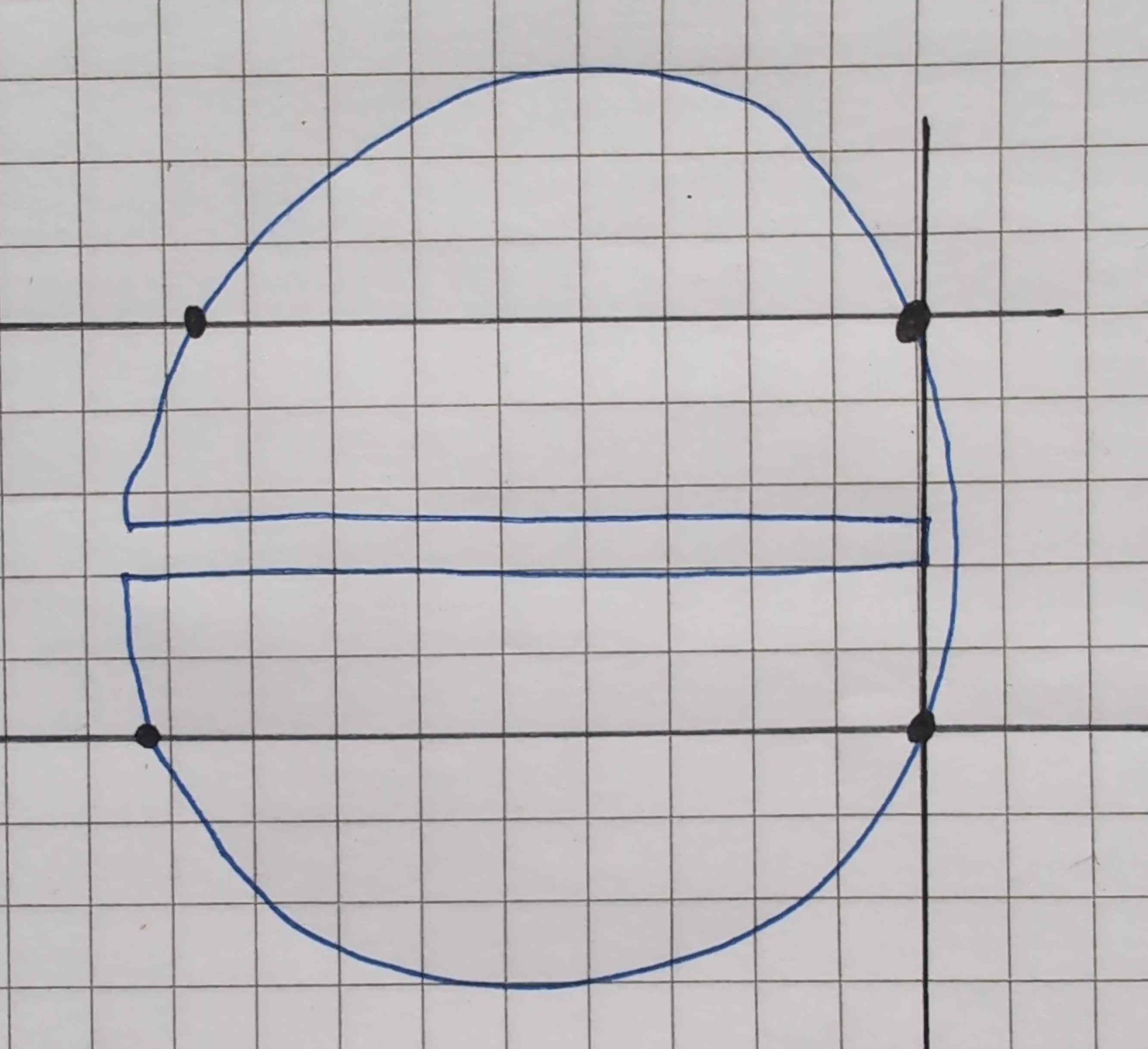
The second insight is that any rectangle must be in between the outliers and the horizontal black lines. If it isn’t, the rectangle will exceed the circle directly above/below the outliers.
Let’s outline our part two solution:
(defn part2
"For this puzzle we require some knowledge about our input. Put the
points in desmos' polygon() function and see what I mean.
We split our circle in two parts, north and south. For each
half-circle we discard the input of the other half and find the
biggest circle, with one caveat: the y-limit must be not too far
from our north and south anchors. Again, look at the polygon."
[input]
(let [points (->> input
s/parse-lines
(mapv s/parse-ints))
[outliers _] (outliers points)
north-point (apply max-key last outliers)
south-point (apply min-key last outliers)
nx (first north-point)
sx (first south-point)
ny-limit (y-limit points nx)
sy-limit (y-limit (rseq points) sx)
north-half (filter #(<= (last north-point) (last %) ny-limit) points)
south-half (filter #(>= (last south-point) (last %) sy-limit) points)]
(max (max-size north-point north-half)
(max-size south-point south-half))))Got it? [north|south]-point are the outliers (we’ll get to the outliers fn in a bit). [n|s]y-limit are the heights of the horizontal lines. We can then limit our search to the points below this line and take the maximum rectangle. Helper functions for part two:
(defn- outliers [points]
(reduce
(fn [[outliers [x y :as prev]] [x' y' :as next]]
(cond
(< 10 (/ x x')) [(conj outliers prev) next]
(< 10 (/ x' x)) [(conj outliers next) next]
:else [outliers next]))
[[] (first points)]
(rest points)))
(defn- y-limit [points x-cutoff]
(->> points
(take-while #(> (first %) x-cutoff))
last
last))
(defn- max-size [anchor points]
(->> points
(map #(size % anchor))
(reduce max)))Day 10: Factory
Part 1
Part 1 is rather straightforward, though the code is perhaps a bit too verbose. The idea is to try all possible combinations of buttons (via combo/combinations) of length n. If this combination of buttons results in the target string, return n. If n starts at 1, we guarantee that we find an optimal solution.
First we parse the line, which is a fn we’re also going to need in part two:
(defn- parse-line [line]
(let [[indicator & buttons] (str/split line #" ")
indicator (-> indicator
(str/replace #"\[" "")
(str/replace #"\]" ""))
joltage (->> (last buttons)
s/parse-ints)
buttons (->> (butlast buttons)
(map s/parse-ints))]
{:indicator indicator :buttons buttons :joltage joltage}))Then part one, where the bulk is done by amount-indicator.
(defn- toggle [x]
(condp = x
\. \#
\# \.))
(defn- press-button
"Presses a button, which is a list of indices.
For example, with indicator: `.##.` and button `(0 2)`, this will
output `##..` (though a vector)."
[indicator idxs]
(reduce (fn [acc i]
(update acc i toggle))
indicator
idxs))
(defn- press-buttons [indicator buttons]
(reduce press-button (vec indicator) buttons))
(defn- amount-indicator
"Computes the minimum amount of button presses necessary to obtain a
given indicator by brute-forcing every possible combination."
[data]
(let [ind (:indicator data)
empty-ind (apply str (repeat (count ind) \.))]
(loop [n 1]
(let [btns (combo/combinations (:buttons data) n)]
(if (not (empty? (filter #(= ind (apply str (press-buttons empty-ind %)))
btns)))
n
(recur (inc n)))))))
(defn part1 [input]
(->> input
s/parse-lines
(map parse-line)
(map amount-indicator)
(reduce +)))Part 2
Part two is really difficult, I could not get this to work on my own. Much later I found this solution by DelightfulCodeWeasel, which is remarkably simple: I might convert my solution to use his insight. Nonetheless, inspired by others I turned to an external solver: ojAlgo. The documentation is in Javadoc and by examples on the website. I couldn’t easily read Javadoc via M-x cider-doc and the examples are either very simple or do something very specific, so this took me a few tries.
The idea is to encode the puzzle in a model and solve it by minimizing some constraints - in this case, minimize the button presses. Here’s the code, but I immediately forgot (rather, never entirely understood) how exactly the ExpressionsBasedModel works, so don’t press me on this.
(defn- solve [buttons joltage]
(let [nb (count buttons)
nj (count joltage)
model (ExpressionsBasedModel.)]
(doseq [b (range nb)]
(doto (.addVariable model)
(.lower 0)
(.weight 1)
(.integer true)))
(doseq [j (range nj)]
(let [expr (.addExpression model)]
(.level expr (get joltage j))
(doseq [b (range nb)]
(when (some #{j} (get buttons b))
;; connect button b to constraint j
(.set expr b 1)))))
(let [result (.minimise model)
state (.getState result)]
;; (.intValue) sometimes get things wrong, 2.9999999994 becomes
;; 2, round ourselves
(vec (for [i (range nb)]
(Math/round (.doubleValue (.get result i))))))))
(defn part2 [input]
(let [problems
(->> input
s/parse-lines
(map parse-line))]
(->> problems
(pmap (fn [problem]
(solve (vec (:buttons problem)) (:joltage problem))))
(map #(reduce + %))
(reduce +))))Day 11: Reactor
Part 1
Rather simple, find out how many paths are from you to out. We start at you and for each child count the paths that end up at out. Effectively a BFS, made fast using memoize.
(defn- parse-input [input]
(->> input
s/parse-lines
(map #(re-seq #"\w+" %))
(map (fn [[from & to]] [from to]))
(into {})))
(defn- count-paths-to-goal
[m cur goal]
(if (= cur goal)
1
(let [neighbours (m cur)]
(reduce + (map #(count-paths-to-goal m % goal)
neighbours)))))
(def count-paths-to-goal (memoize count-paths-to-goal))
(defn part1 [input]
(count-paths-to-goal (parse-input input) "you" "out"))Part 2
Very similar, but with a few constraints. How many paths go from svr to out, passing through both dac and fft. We know the graph is acyclic by virtue of part one actually terminating. This means that each valid path either goes from fft -> dac or from dac -> fft somewhere. We know which of these two options is the case by checking if there is at least one path from from fft to dac.
Let’s assume for now it’s the first one. Then the result is (* (p :svr :fft) (p :fft :dac) (p :dac :out)), where p counts the amount of paths from its first argument to its second. This is effectively the solution. All that remains is to remove our assumption and check which of the two paths we’re dealing with:
(defn part2 [input]
(let [g (parse-input input)
[first second] (if (pos? (count-paths-to-goal g "fft" "dac"))
["fft" "dac"]
["dac" "fft"])]
(* (count-paths-to-goal g "svr" first)
(count-paths-to-goal g first second)
(count-paths-to-goal g second "out"))))Day 12: Christmas Tree Farm
The last day already! This day only has one part, which looks remarkably difficult, but is remarkably easy. It is in fact not too strange that it is easy, since it would very difficult if it was as difficult as it looks. It’s essentially a version of the 2D bin packing problem, which is NP-hard. Take a look at the first line in our input:
40x42: 38 37 45 42 54 41
We have a 40x42 grid, and we have to check whether we can fit 257 3x3 shapes in it. This is pretty hard in general. However, some cases are trivially solvable or trivially not solvable: when the grid is simply big enough to put each shape next to each other.
Let’s try this solution first:
(defn naive-fit? [recipe]
(let [[grid presents] (str/split recipe #": ")
gridsize (reduce * (s/parse-ints grid))
presentsize (* 9 (reduce + (s/parse-ints presents)))]
(>= gridsize presentsize)))
(defn part1 [input]
(->> input
s/parse-blocks
last
s/parse-lines
(filter naive-fit?)
count))This returns the amount of problems that are trivially solvable. And it turns out that this is the correct solution! Phew!