AoC 2022
My solutions for Advent of Code 2022
Welcome to my solution page for Advent of Code 2022. You can find the git repo here.
Day 1: Calorie Counting
Part 1
Straightforward, group, sum each group, take max group
(defn part1 [input]
(->> (s/parse-blocks input)
(map s/parse-ints)
(map #(reduce + %))
(apply max)))Part 2
Take max 3 and sum those.
(defn part2 [input]
(->> (s/parse-blocks input)
(map s/parse-ints)
(map #(reduce + %))
(sort >)
(take 3)
(reduce +)))Day 2: Rock Paper Scissors
Part 1
Rock paper scissors. Let’s first define some constant mappings:
(def shape-score {:rock 1, :paper 2, :scissors 3})
(def outcome-score {:loss 0, :draw 3, :win 6})
(def beats {:rock :scissors, :paper :rock, :scissors :paper})
(def beaten-by (map-invert beats))
(def opponent-map {"A" :rock, "B" :paper, "C" :scissors})
(def you-map {"X" :rock, "Y" :paper, "Z" :scissors})And now we need to find out what the outcome of each round is and sum the score:
(defn- outcome [opponent you]
(cond
(= opponent you) :draw
(= (beats you) opponent) :win
:else :loss))
(defn- score-round [opponent you]
(+ (shape-score you)
(outcome-score (outcome opponent you))))
(defn part1 [input]
(->> (s/parse-lines input)
(map #(str/split % #" "))
(map (fn [[o y]]
(score-round (opponent-map o) (you-map y))))
(reduce +)))Part 2
We need to choose the shape based on the outcome, and then score the round:
(def instruction-map {"X" :loss, "Y" :draw, "Z" :win})
(defn choose-shape [opponent instruction]
(case instruction
:draw opponent
:win (beaten-by opponent)
:loss (beats opponent)))
(defn part2 [input]
(->> (s/parse-lines input)
(map #(str/split % #" "))
(map (fn [[o i]]
(let [opp (opponent-map o)
instr (instruction-map i)
you (choose-shape opp instr)]
(score-round opp you))))
(reduce +)))Day 3: Rucksack Reorganization
Part 1
Group each line in two parts, take the intersection of each part, and score that.
(defn- split-in-two [v]
(let [c (count v)
h (quot c 2)]
[(subvec v 0 h) (subvec v h)]))
(defn- common-items [& vecs]
(apply set/intersection (map set vecs)))
(defn- char-to-num [c]
(if (Character/isUpperCase c)
(- (int c) 38)
(- (int c) 96)))
(defn part1 [input]
(->> (s/parse-lines input)
(map vec)
(map split-in-two)
(mapcat #(apply common-items %))
(map char-to-num)
(reduce +)))Part 2
Instead of splitting each line in to ((map split-in-two)), we take groups of three lines ((partition 3)) and do the same computation.
(defn part2 [input]
(->> (s/parse-lines input)
(map vec)
(partition 3)
(mapcat #(apply common-items %))
(map char-to-num)
(reduce +)))Day 4: Camp Cleanup
Part 1
The following function tests whether two ranges \(r_1, r_2\) fully overlap:
(defn- fully-overlap? [[s1 e1 :as r1] [s2 e2 :as r2]]
(cond
(= e1 e2) true
(> e1 e2) (<= s1 s2)
(< e1 e2) (>= s1 s2)))This image shows one scenario for when the ranges fully overlap, and in dotted line when they don’t overlap:
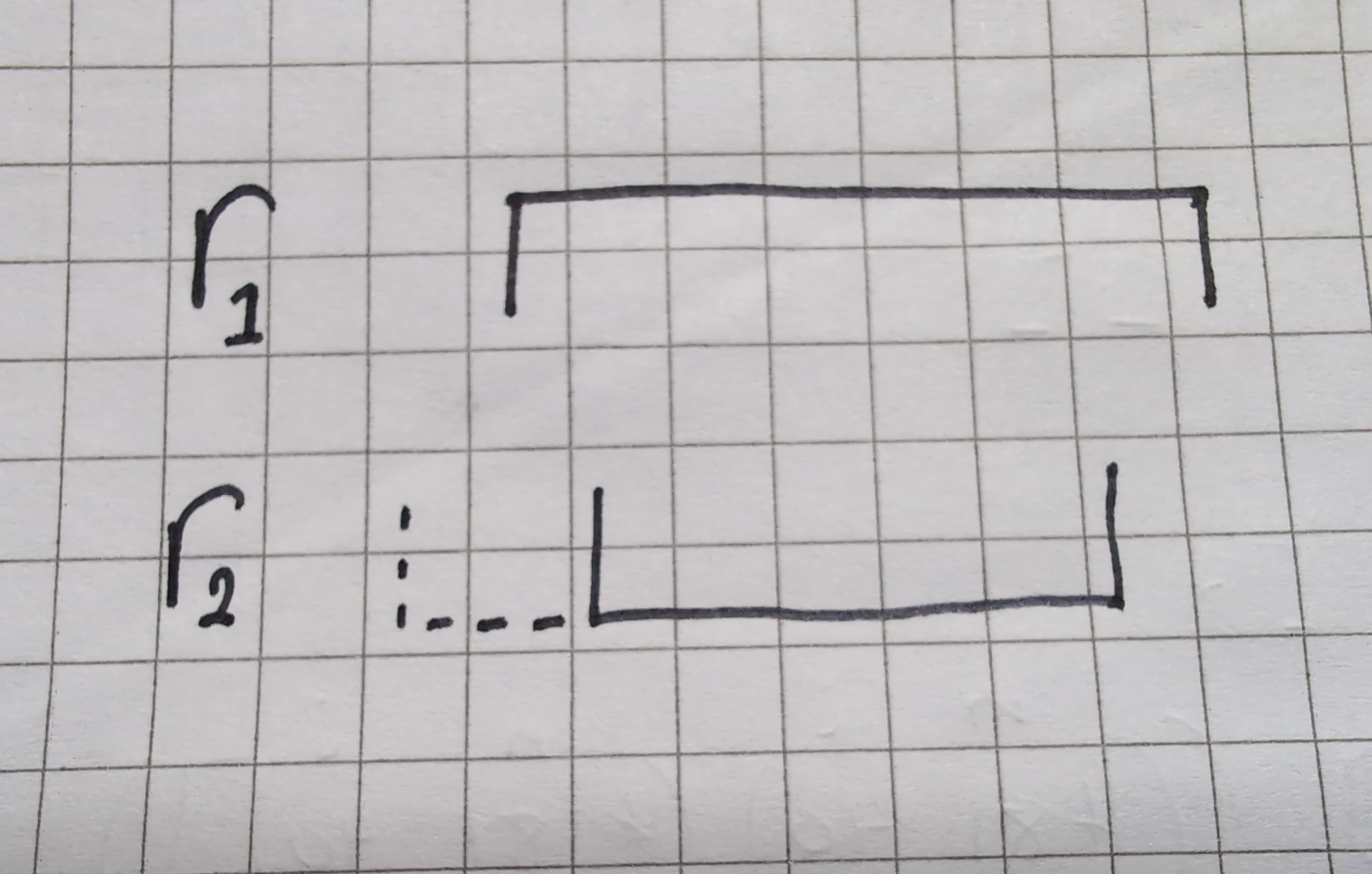
It should be clear that if \(e_1 > e_2\), the ranges fully overlap if and only if \(s1 <= s2\). The opposite case is symmetric, of course. This makes part 1 easy:
(defn part1 [input]
(->> (s/parse-lines input)
(map #(str/split % #","))
(map s/parse-ranges)
(filter #(apply fully-overlap? %))
count))Part 2
This should be straightforward, if not look at the dotted line above.
(defn- partly-overlap? [[s1 e1] [s2 e2]]
(cond
(= e1 e2) true
(> e1 e2) (>= e2 s1)
(< e1 e2) (>= e1 s2)))
(defn part2 [input]
(->> (s/parse-lines input)
(map #(str/split % #","))
(map s/parse-ranges)
(filter #(apply partly-overlap? %))
count))Day 5: Supply Stacks
Part 1
First, let’s parse properly. I want each a list of sequences: the list of stacks of crates.
(defn parse-crates
"Takes a block and returns the columns of crate letters."
[block]
(let [rows (-> block s/parse-lines butlast)
cols (v/transpose rows)]
(keep-indexed
(fn [i col]
(when (= 1 (mod i 4))
(remove #{\space} col)))
cols)))
(defn- parse-procedure [line]
(let [[_ a f t] (re-find #"move (\d+) from (\d+) to (\d+)" line)]
{:amount (parse-long a)
:from (dec (parse-long f))
:to (dec (parse-long t))}))
(defn- parse-procedures [block]
(map parse-procedure (s/parse-lines block)))We parse the crates like this:
(aoc.2022.day05/parse-crates
" [D]
[N] [C]
[Z] [M] [P]
1 2 3
")((\N \Z) (\D \C \M) (\P))We now have to apply each procedure, one by one, and find the result (the character of the crate that ends up on top of each stack).
See the following two parts:
(conj '(1 2 3) 4)(4 1 2 3)(drop 2 '(1 2 3 4 5 6))(3 4 5 6)Which is fantastic, since we can just conj and drop and the stacks will be moved as they should, one-by-one. Here’s the rest of part one:
(defn- apply-procedure
"Applies a procedure to a list of stacks."
[crane stacks {:keys [amount from to]}]
(let [src (nth stacks from)
tomove (take amount src)
tomove (if (= crane :CrateMover9001) (reverse tomove) tomove)]
(-> stacks
vec
(assoc from (drop amount src))
(update to #(apply conj % tomove)))))
(defn- result [input crane]
(let [[crates-block procedures-block] (s/parse-blocks input)]
(->> (parse-procedures procedures-block)
(reduce (partial apply-procedure crane)
(parse-crates crates-block))
(map first)
(apply str))))
(defn part1 [input] (result input :CrateMover9000))This is of course not my initial iteration, as you might see from the CraneMover9001. Oops, spoilers for
Part 2
(defn part2 [input] (result input :CrateMover9001))Day 6: Tuning Trouble
Part 1
Partition input in groups of 4, continue until a group has only unique characters. This check is done by (not= n (count (distinct group))), where \(n=4\) for part one. Then we add \(n\) to find the first character where this check holds, not just the first group.
(defn- first-unique-group [input n]
(->> input
(partition n 1)
(take-while #(not= n (count (distinct %))))
count
(+ n)))
(defn part1 [input] (first-unique-group input 4))Part 2
(defn part2 [input] (first-unique-group input 14))Day 7: No Space Left On Device
Part 1
This was an interesting day. A quick check in the input reveals that the only $ cd / is at the beginning of the terminal output. This means that we can keep track of the current working directory (pwd) and treating that as a stack. $ cd a pushes a on the stack, $ cd .. pops the current directory from the stack.
We ignore the $ ls and dir a output lines. Whenever we find a file with corresponding size, we add the filesize to each directory in pwd.
(defn- pts [pwd]
(apply str (reverse pwd)))
(defn- directory-sizes [input]
(let [[pwd dir-sizes]
(reduce
(fn [[pwd dir-sizes] line]
(condp re-matches line
#"\$ ls" [pwd dir-sizes]
#"dir \w+" [pwd dir-sizes]
#"\$ cd \.\." [(pop pwd) dir-sizes]
#"\$ cd /" [(conj pwd "/") (assoc dir-sizes "/" 0)]
#"\$ cd ([\w]+)"
:>> (fn [[_ dir]]
(let [d (str dir "/")
pwd' (conj pwd d)]
[pwd' (assoc dir-sizes (pts pwd') 0)]))
#"([0-9]+) .+"
:>> (fn [[_ filesize-str]]
(let [filesize (parse-long filesize-str)]
;; add filesize to current directory and all
;; parent dirs (in pwd)
[pwd
(loop [sizes dir-sizes
pwd' pwd]
(if (empty? pwd')
sizes
(recur
(update sizes (pts pwd') #(+ filesize %))
(rest pwd'))))]))))
['() {}]
(s/parse-lines input))]
dir-sizes))And part one is just summing the sizes of all directories less than size \(100000\):
(defn part1 [input]
(let [sizes (directory-sizes input)]
(->> sizes
(filter #(> 100000 (last %)))
(map last)
(reduce +))))Part 2
Part two is easy now that we’re properly tracking directory sizes:
(defn part2 [input]
(let [sizes (directory-sizes input)
used-space (sizes "/")
unused-space (- 70000000 used-space)
deletion-size (- 30000000 unused-space)
]
(->> sizes
(sort-by val)
(drop-while #(> deletion-size (val %)))
first
val)))Day 8: Treetop Tree House
Part 1
Grid traversing. From the puzzle text:
A tree is visible if all of the other trees between it and an edge of the grid are shorter than it.
“all other trees between it and an edge of the grid” is obtained via this snippet:
[(subvec col 0 y)
(subvec col (inc y))
(subvec row 0 x)
(subvec row (inc x))]Now part one is not too difficult:
(defn- visible? [grid [x y]]
(let [row (g/row grid y)
col (g/col grid x)
z (g/cell grid [x y])
all-lower? (fn [coll]
(every? #(> z %) coll))]
(or (all-lower? (subvec col 0 y))
(all-lower? (subvec col (inc y)))
(all-lower? (subvec row 0 x))
(all-lower? (subvec row (inc x))))))
(defn part1 [input]
(let [g (g/to-matrix input #(parse-long (str %)))]
(count
(for [y (range (g/height g))
x (range (g/width g))
:when (visible? g [x y])]
[x y]))))Part 2
In part two we compute the score, which is a similar process. Say that a tree \(t\) has x-coordinate \(x\), and the grid has width \(w\). Then we check the tree at \(x+1\), \(x+2\), \(x+3\), etc. Whenever the tree at \(x+i\) is at least as high as \(t\), or \(x+i > w\), we return \(i\).
In our code, we use (take-while $(> z %)), which means that we exclude \(x+i\) in the process above, and only go to \(x+i-1\). In that case, we must increment our result. The rest of the process is trivial:
(defn- score [grid [x y]]
(let [row (g/row grid y)
col (g/col grid x)
z (g/cell grid [x y])
num-lower-trees
(fn [coll]
(let [res
(->> coll
(take-while #(> z %))
count)]
;; if there is one, include the tree that's higher, since
;; we can see that.
(if (= res (count coll))
res
(inc res))))]
(* (num-lower-trees (reverse (subvec col 0 y)))
(num-lower-trees (subvec col (inc y)))
(num-lower-trees (reverse (subvec row 0 x)))
(num-lower-trees (subvec row (inc x))))))
(defn part2 [input]
(let [g (g/to-matrix input #(parse-long (str %)))]
(->>
(for [y (range (g/height g))
x (range (g/width g))]
[[x y] (score g [x y])])
(map last)
(apply max))))